Line Continuity or Discontinuity Do in a Composition Art

Contents:

1. What is a Discontinuous Function?
2. Graph of a Discontinuous Function
3. Finding Discontinuities
4. Types of Discontinuity
   • Essential Discontinuity (Irremovable)
   • Infinite Discontinuity
   • Jump (Pace) Aperture
   • Oscillating Aperture
   • Removable (Pigsty) Discontinuity

What is a Discontinuous Part?

A discontinuous role is a function which is not continuous at one or more than points. Almost functions are, perhaps surprisingly, discontinuous in i way or some other [1].

Existence "continuous at every betoken" means that at every indicate a:

1. The part exists at that point. If you can plug an ten-value into your part and it returns a value, it'due south continuous at that point.
2. The limit of the part as x goes to the point a exists. In other words, the function values surrounding point "a" are all approaching the same number.
3. Both (1) and (2) are equal.

In notation, we tin can write that every bit:

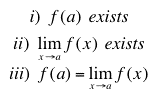
In plain English, what that means is that the function passes through every point, and each indicate is close to the next: there are no drastic jumps (dissimilar jump discontinuities). When you're cartoon the graph, you can describe the function from left to right without taking your pencil off the paper.

A discontinuous function is one for which yous must take the pencil off the paper at least once while drawing.

Graph of a Discontinuous Office

A spring discontinuity.

Graphically, a discontinuous function volition either accept a hole—ane spot, or several spots, where the function is not defined—or a jump, where the value of f(x) changes ("jumps") quickly as you go from 1 spot to another that is infinitesimally close.

A vertical asymptote. The function will arroyo this line, only never actually bear on it.

Information technology might also have an asymptote, a line where, as the function approaches, it goes to infinity. The role never merges with this line, though it may approach infinitely close.

Dorsum to Top

Finding Discontinuities

If your role can be written equally rational office (i.e. a fraction), any values of ten that brand the denominator go to zippo will exist discontinuities of your part. Those are the places your function is not divers considering of division by zero.

If you lot take a piecewise function, the point where one piece ends and another slice ends are also skilful places to check for discontinuity.

Otherwise, the easiest fashion to notice discontinuities in your function is to graph it. Take note of any holes, asymptotes, or jumps. These all represent discontinuities, and just ane discontinuity is enough to make your function a discontinuous role.

Types of Aperture

Types of Discontinuity.

Classifying types of aperture is more difficult than it appears, due to the fact that different authors classify them in different ways. For example:

• Some authors simplify the types into two umbrella terms: removable (holes) and non-removable (jumps, infinite and essential discontinuities cannot be removed equally they are also far apart or wild in their beliefs).
• Essential discontinuities (that jump about wildly as the function approaches the limit) are sometimes referred to as the "non-removable discontinuity", excluding jumps and infinite from the definition of non-removable.
• Some authors too include "mixed" discontinuities equally a type of discontinuity, where the discontinuity is a combination of more one blazon.

The takeaway: There isn't "one" nomenclature system for types of discontinuity that everyone agrees upon. Which system yous employ volition depend upon the text you are using and the preferences of your instructor. The following list should be taken as a guide, non a prepare in stone classification system.

Back to Top

Essential Discontinuity

1. Essential Discontinuity
2. Essential Singularity

Essential Discontinuity

An essential discontinuity (besides called second type or irremovable discontinuity) is a aperture that jumps wildly as it gets closer to the limit. This makes information technology difficult to remove the gap (hence the alternate name, "irremovable" discontinuity) and perform any calculations on the function.

An essential discontinuity is considered to exist the "worst" of the types of discontinuity. That's because the behavior effectually where the limits should be is abnormal, impossible to calculate, and sometimes simply plain crazy. There might be many jump discontinuities within a very brusk distance, or yous might not be able to pivot down any kind of behavior at all. Graphing calculators might not be whatsoever assistance (considering of the abnormal behavior), and yous might have to resort to pen and newspaper to make whatever sense of the graph.

Subtypes

Essential discontinuities (i.east. non-removable discontinuities) tin exist further cleaved downward into two types of discontinuity, based on whether the i-sided limits are bounded or unbounded (Bauldry, 2011):

• Bounded: oscillatory discontinuity. The pattern near the limit bounces up and down, never forming a blueprint y'all can pin down.
• Unbounded: infinite aperture. The limits exist, but they are infinite, getting larger every bit you move closer to the limit.

Unproblematic (removable) discontinuities can also be broken downwardly into two subtypes:

• A removable discontinuity has a gap that tin easily exist filled in, considering the limit is the same on both sides.
• A jump discontinuity at a point has limits that exist, but information technology'south different on both sides of the gap.

In either of these two cases the limit can be quantified and the gap can be removed; An essential discontinuity can't be quantified. Note that spring discontinuities that happen on a curve tin can't exist removed, and are therefore essential (Rohde, 2012).

Back to Top

Essential Singularity

An essential singularity is an ill-behaved "hole" in a non-analytic circuitous office that tin't exist removed / repaired. In other words, there's no piece of cake fashion to plough a part with an essential singularity into one that's continuous and differentiable.

This blazon of singularity is like to its real-valued counterpart: the essential aperture. These types of singularities / discontinuities are difficult to bargain with because of their pathological behavior at a certain betoken.

Essential singularities are 1 of three types of singularity in complex assay. The other two are poles (isolated singularities) and removable singularities, both of which are relatively well behaved. Essential singularities are classified by exclusion: if it isn't a pole or a removable singularity, then it'due south an essential one.

Example of a Function with an Essential Singularity

The function exp (1/z) has an essential singularity at z = 0, where the function is undefined (considering of division by cipher). At this point, the function does not have a limit, so information technology's incommunicable to remove the singularity.

Hue-luminance plot of exp(one/z), centered on the essential singularity at zero. The function behaves differently depending on which direction you approach the office from. Credit: Functor Salad | Wikimedia Commons./>

In Terms of the Laurent Series

Essential discontinuities can be identified by looking at the behavior of a Laurent series representing the neighborhood around a singularity. Specifically, a singularity is essential if the master part of the Laurent series has infinitely many nonzero terms (Kramer, n.d.).

Principal part of the Laurent serial.

Back to Pinnacle

Infinite Aperture

An infinite discontinuity has i or more space limits—values that go larger and larger as you movement closer to the gap in the function. An space aperture is a subtype of essential discontinuities, which are a broad set of desperately behaved discontinuities that cannot exist removed.

Types of Discontinuity. The infinite discontinuity on the right has function values that keep on going towards infinity.

This function but tends to infinity at ten = 0 on one side (the right), but information technology'southward still classified as an infinite discontinuity.

It's important to notation that merely one side has to tend to ±infinity in guild for the discontinuity to exist classified as space. 1 side may accomplish a sure function value, or be undefined. But as long as one side is either negative infinity or positive infinity, then it'southward an infinite discontinuity.

Infinity can exist Positive or Negative

The office tin become towards infinity in the aforementioned direction, or in different directions. For instance, the function can go towards:

• Positive infinity on both sides,
• Negative infinity on both sides, or
• One side can go to negative infinity and the other towards positive infinity.

Graph of y = one/ten, which tends towards both negative and positive infinity at x = 0.

Graph of 1/10², which tends towards negative infinity in both directions at x = 0. (Graphs made with the Desmos Figurer)

Back to Top

Leap Aperture

A jump discontinuity (also called a pace aperture or discontinuity of the starting time kind) is a gap in a graph that jumps abruptly.

The following graph jumps at the origin (x = 0).

In club for a discontinuity to be classified as a spring, the limits must:

1. exist as (finite) existent numbers on both sides of the gap, and
2. cannot be equal. If the limits are equal, it's a pigsty, not a jump (more than formally, holes are called removable discontinuities).

The departure betwixt the two limits is the spring at that point (Sohrab, 2003). Surprisingly, the number of jumps in whatever detail function are countable; In other words, it'south non possible to take an infinite number of jumps, fifty-fifty in continuous functions (Sohrab, 2003).

When do Jumps Happen?

A spring discontinuity unremarkably only happens in piecewise or step functions.

Piecewise functions are defined on a sequence of intervals.

Instance of a step function (the ruby graph). This particular pace office is right-continuous.

Step functions are a sub-type of piecewise functions, where there'due south a series of identical "staircase" steps.

Notation for Jump Discontinuities

In notation, a jump discontinuity can be defined in terms of limits on either side of the bound. Let's say you have a function, f(t), which has a spring discontinuity at t = 10. The following notation describes the jump:

Left limit:

Correct limit:

The jump itself tin be defined in terms of the two limits:
f (10 +) – f (10 -).

Jump vs. Footstep

Although "pace discontinuity" is a fairly common term, it tends to exist an informal ane. The usual name for this type of discontinuity is a jump aperture. However, when information technology looks like a physical step, it makes sense to phone call it that (rather than a jump, which would bring to listen a large gap in the horizontal centrality, which isn't always the instance!). Which term y'all utilise is usually a thing of personal pick, or the pick of your instructor.

Examples of Pace Discontinuity / Jump Discontinuity

The office

has a jump aperture when x = one. There is no single limit at this point; fifty-fifty though the one sided limits Fifty^– and L⁺ both exist, considering they are non equal. If you imagined walking along the curve, you would have to do some serious jumping when you got to one. This is illustrated below.

In the graph below, in that location is a footstep discontinuity at -4, because the left and right paw limits both be and are not infinite but are different. At 2 there is another pace discontinuity; the right limit is -ane and the left limit is five. The discontinuity at 4, however, is not a step aperture because the left and correct manus limits are equal. This is another type of discontinuity—a removable aperture.

Back to Tiptop

What is an Aquiver Aperture?

An oscillating discontinuity (also called an infinitely oscillating discontinuity) jumps well-nigh wildly (i.east. oscillates) as it approaches the limit; there'south no fashion to "repair" the discontinuity. It's often defined by exclusion: information technology isn't a removable discontinuity, a spring aperture, or an infinite aperture. Therefore, y'all might see it referred to every bit an "other" type of discontinuity.

Bounded and Unbounded Functions

Oscillating discontinuities are bounded. In other words, their oscillations stay between certain lines. For example, the function might be divisional between a high point of y = 3 and a low point of y = -3. If the office is unbounded at one or both sides, it'south an infinite aperture. In other words, the office must be completely bounded at all points in order for there to exist an oscillating aperture. In add-on, the i sided limits do non exist at all.

Example

Perhaps non surprisingly, many oscillating functions have at least one oscillating discontinuity.

It's impossible to pivot down a limit for the function sin(1/x) at cypher.

Oscillating discontinuities are a sub-type of essential, or non-repairable, discontinuities.

How to Notice an Oscillating Aperture

The easiest way to identify this type of discontinuity is by continually zooming in on a graph: no matter how many times yous zoom in, the function will continue to oscillate around the limit.

On the TI-89, graph the function in a modest window (for example, a [-2,2,i]*[-2, 2, 1] window. Press the Zoom key, select the Zoom Box characteristic (1:ZBox) and press Enter. Marking the upper left of the box by pressing Enter, so enlarge the box using the arrow keys. Printing Enter again. Echo ad infinitum. For full instructions and images of how to do this, meet: Module 8: Continuity on the TI website.

Back to Superlative

What is a Removable Discontinuity?

A removable aperture (as well called a hole discontinuity) has a gap that tin easily exist filled in, because the limit is the same on both sides. You can think of information technology as a small hole in the x-axis.

A removable discontinuity is sometimes chosen a betoken discontinuity, because the role isn't defined at a single (miniscule point).

Removing The Pigsty

The pigsty is called a removable aperture because it can be filled in, or removed, with a fiddling redefining of the part's values. But replace the function value at the hole with the value of the limit.

Instance

Take the post-obit piecewise function:

Graphed, the function looks like this:

Note the modest hole at x = 0.5. The office value here (i.eastward. the y-value) is 4, creating a problem if we want to perform further calculations on the function (similar integration, for example).

On the graph, you can just pencil the hole in and remove the dot at (0.5, 4). Mathematically, if nosotros take the y-values very close to the pigsty, we can fill it in that fashion. The piecewise function is given as h(x) = 1.5 + 1 / (x + .25) for every point except 0.five, so we can ignore that quirk and simply use the function to fill in the hole. Substituting x = 0.5 into the role, we get:
h(x) = 1.5 + 1 / (0.5 + .25) = 17/six ≈ 2.83.

Types of Discontinuity: References

Image: Functor Salad [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]

[1] Drago et. al. A "Boutonniere" of Discontinuous Functions for Beginners in Mathematical Analysis. Retrieved July 13, 2021 from: http://ceadserv1.nku.edu/longa//classes/mat420/days/highlights/PathologicalFunctions.pdf
[2] Department 1.4. Continuity. Retrieved July xiii, 2021 from: https://www.math.uh.edu/~beatrice/143114.pdf

Bauldry, W. (2011). Introduction to Real Analysis: An Educational Approach. John Wiley & Sons.
Bogley, W. (1996). Removable Discontinuities. Retrieved Oct 28, 2019 from: https://oregonstate.edu/instruct/mth251/cq/Stage4/Lesson/removable.html
Grigoriu, Thou. Stochastic Calculus: Applications in Science and Engineering.
Infinite Discontinuity. Retrieved October 29, 2019 from: http://www-math.mit.edu/~djk/18_01/chapter02/example03.html
Infinite Discontinuities. Retrieved October 28, 2019 from: https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-autumn-2010/ane.-differentiation/office-a-definition-and-basic-rules/session-5-aperture/MIT18_01SCF10_Ses5c.pdf
Knopp, K. "Essential and Not-Essential Singularities or Poles." §31 in Theory of Functions Parts I and 2, Ii Volumes Bound every bit 1, Part I. New York: Dover, pp. 123-126, 1996.
Kramer, P. L.S. Examples. Retrieved August 22, 2020 from: http://eaton.math.rpi.edu/faculty/Kramer/CA13/canotes111113.pdf
Krantz, S. Yard. "Removable Singularities, Poles, and Essential Singularities." §4.1.four in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 42, 1999.
Rohde,U. et al. (2012). Introduction to Differential Calculus: Systematic Studies with Engineering Applications for Beginners. John Wiley and Sons.
Sohrab, H. (2003). Basic Real Analysis. Springer Science and Business organization Media.
Thomson, B. et al., (2008). Elementary Real Analysis, Volume ane. ClassicalRealAnalysis.com.
Wineman, A. & Rajagopal, K. (2000). Mechanical Response of Polymers: An Introduction. Cambridge University Press.

Desmos Calculator.

---------------------------------------------------------------------------

Need aid with a homework or examination question? With Chegg Study, you can go stride-by-pace solutions to your questions from an good in the field. Your first 30 minutes with a Chegg tutor is free!

smithinscurs1969.blogspot.com

Source: https://www.calculushowto.com/calculus-definitions/types-of-discontinuity/

Share this post